梯度下降算法以及其Python实现
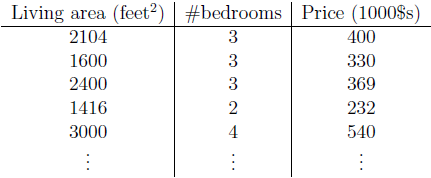
为了实现监督学习,我们选择采用自变量x1、x2的线性函数来评估因变量y值,得到:
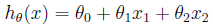
这里,sita1、sita2代表自变量x1、x2的权重(weights),sita0代表偏移量。为了方便,我们将评估值写作h(x),令x0=1,则h(x)可以写作:
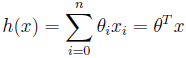
其中n为输入样本数的数量。为了得到weights的值,我们需要令我们目前的样本数据评估出的h(x)尽可能的接近真实y值。我们定义误差函数(cost function)来表示h(x)和y值相接近的程度:
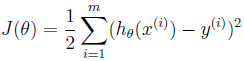
这里的系数1/2是为了后面求解偏导数时可以与系数相互抵消。我们的目的是要误差函数尽可能的小,即求解weights使误差函数尽可能小。首先,我们随机初始化weigths,然后不断反复的更新weights使得误差函数减小,直到满足要求时停止。这里更新算法我们选择梯度下降算法,利用初始化的weights并且反复更新weights:
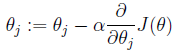
这里a代表学习率,表示每次向着J最陡峭的方向迈步的大小。为了更新weights,我们需要求出函数J的偏导数。首先计算只有一个数据样本(x,y)时,如何计算J的偏导数:
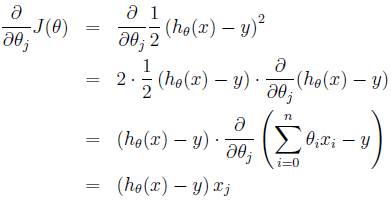
对于只含有一组数据的训练样本,我们可以得到更新weights的规则为:
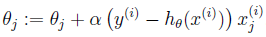
扩展到多组数据样本,更新公式为:
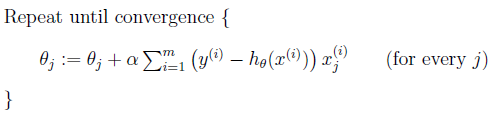
称为批处理梯度下降算法,这种更新算法所需要的运算成本很高,尤其是数据量较大时。考虑下面的更新算法:

该算法又叫做随机梯度下降法,这种算法不停的更新weights,每次使用一个样本数据进行更新。当数据量较大时,一般使用后者算法进行更新。
二、梯度下降Python实现
自己创建了一组数据,存为csv格式,如下图所示:
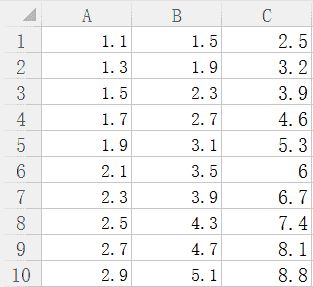
待训练数据A、B为自变量,C为因变量。
在写程序之前,要先导入我们需要的模块。
|
1
2
|
import numpy as np
from numpy import genfromtxt
|
首先将数据读入Python中,程序如下所示:
|
1
2
|
dataPath = r“E:learninghouse.csv”
dataSet = genfromtxt(dataPath, delimiter=‘,’)
|
接下来将读取的数据分别得到自变量矩阵和因变量矩阵:
|
1
2
3
4
5
6
|
def getData(dataSet):
m, n = np.shape(dataSet)
trainData = np.ones((m, n))
trainData[:,:–1] = dataSet[:,:–1]
trainLabel = dataSet[:,–1]
return trainData, trainLabel
|
这里需要注意的是,在原有自变量的基础上,需要主观添加一个均为1的偏移量,即公式中的x0。原始数据的前n-1列再加上添加的偏移量组成自变量trainData,最后一列为因变量trainLabel。
下面开始实现批处理梯度下降算法:
|
1
2
3
4
5
6
7
8
|
def batchGradientDescent(x, y, theta, alpha, m, maxIterations):
xTrains = x.transpose()
for i in range(0, maxIterations):
hypothesis = np.dot(x, theta)
loss = hypothesis – y
gradient = np.dot(xTrains, loss) / m
theta = theta – alpha * gradient
return theta
|
x为自变量训练集,y为自变量对应的因变量训练集;theta为待求解的权重值,需要事先进行初始化;alpha是学习率;m为样本总数;maxIterations为最大迭代次数;
求解权重过程,初始化batchGradientDescent函数需要的各个参数:
|
1
2
3
4
5
|
trainData, trainLabel = getData(dataSet)
m, n = np.shape(trainData)
theta = np.ones(n)
alpha = 0.05
maxIteration = 1000
|
alpha和maxIterations可以更改,之后带入到batchGradientDescent中可以求出最终权重值。
|
1
|
theta = batchGradientDescent(trainData, trainLabel, theta, alpha, m, maxIteration)
|
之后我们给出一组数据,需要进行预测,预测函数:
|
1
2
3
4
5
6
|
def predict(x, theta):
m, n = np.shape(x)
xTest = np.ones((m, n+1))
xTest[:, :–1] = x
yPre = np.dot(xTest, theta)
return yPre
|
x为待预测值的自变量,thta为已经求解出的权重值,yPre为预测结果
我们给出测试集
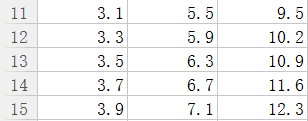
对该组数据进行预测,程序如下:
|
1
2
|
x = np.array([[3.1, 5.5], [3.3, 5.9], [3.5, 6.3], [3.7, 6.7], [3.9, 7.1]])
print predict(x, theta)
|
输出结果如下:
|
1
|
[9.49608552 10.19523475 10.89438398 11.59353321 12.29268244]
|
我们可以更改学习率和迭代次数进行预测结果的对比:
更改学习率由0.05变为0.1时,结果为:
|
1
|
[ 9.49997917 10.19997464 10.89997012 11.59996559 12.29996106]
|
发现预测结果要由于学习率为0.05时,这说明学习率0.05选择的偏小,即每一次迈步偏小。
固定学习率为0.05,更改迭代次数为5000时,结果为:
|
1
|
[ 9.5 10.2 10.9 11.6 12.3]
|
这正是我们想要的预测结果,这说明有限循环次数内,循环次数越多,越接近真实值。但是也不能无限循环下去,需要寻找一个度。
一般达到以下的任意一种情况即可以停止循环:
1.权重的更新低于某个阈值;
2.预测的错误率低于某个阈值;
3.达到预设的最大循环次数;
其中达到任意一种,就停止算法的迭代循环,得出最终结果。
完整的程序如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
#coding=utf-8
import numpy as np
import random
from numpy import genfromtxt
def getData(dataSet):
m, n = np.shape(dataSet)
trainData = np.ones((m, n))
trainData[:,:–1] = dataSet[:,:–1]
trainLabel = dataSet[:,–1]
return trainData, trainLabel
def batchGradientDescent(x, y, theta, alpha, m, maxIterations):
xTrains = x.transpose()
for i in range(0, maxIterations):
hypothesis = np.dot(x, theta)
loss = hypothesis – y
# print loss
gradient = np.dot(xTrains, loss) / m
theta = theta – alpha * gradient
return theta
def predict(x, theta):
m, n = np.shape(x)
xTest = np.ones((m, n+1))
xTest[:, :–1] = x
yP = np.dot(xTest, theta)
return yP
dataPath = r“E:learninghouse.csv”
dataSet = genfromtxt(dataPath, delimiter=‘,’)
trainData, trainLabel = getData(dataSet)
m, n = np.shape(trainData)
theta = np.ones(n)
alpha = 0.1
maxIteration = 5000
theta = batchGradientDescent(trainData, trainLabel, theta, alpha, m, maxIteration)
x = np.array([[3.1, 5.5], [3.3, 5.9], [3.5, 6.3], [3.7, 6.7], [3.9, 7.1]])
print predict(x, theta)
|
我是一个机器学习的小白,刚刚开始接触,从最基本的也是很重要的梯度下降开始学习。这篇文章是我对梯度下降的理解,还有很多不完善的地方,我只给出了批量梯度下降算法的python实现,随机梯度下降还需要我进一步编写,而且关于循环停止,本文只是最简单的循环次数停止,等等,还有很多问题,以后会继续更近并改进该文章。写下来就是为了随时随地翻出来看看,巩固知识,并不断改进。
转载自演道,想查看更及时的互联网产品技术热点文章请点击http://go2live.cn