一致性hash算法
[TOC]
一致性hash算法。用于解决memcached/redis 增减服务器时,尽量保持key依然命中之前的server的解决方案。
场景
假设我们有一个网站,最近发现随着流量增加,服务器压力越来越大,之前直接读写数据库的方式不太给力了,于是我们想引入Memcached作为缓存机制。现在我们一共有三台机器可以作为Memcached服务器,如下图所示。
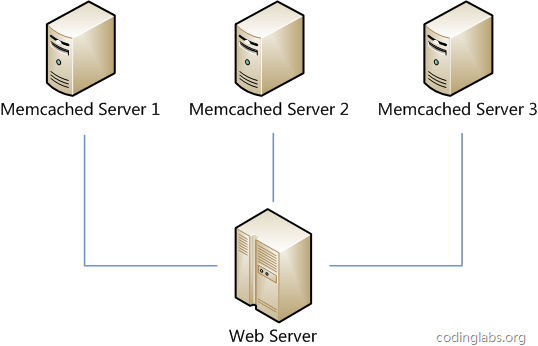
默认实现
默认实现:相同key的访问会被发送到相同的服务器。很多方法可以实现这一点,最常用的方法是计算哈希。例如对于每次访问,可以按如下算法计算其哈希值:
h = Hash(key) % 3
其中Hash是一个从字符串到正整数的哈希映射函数。这样,如果我们将Memcached Server分别编号为0、1、2,那么就可以根据上式和key计算出服务器编号h,然后去访问。
这个方法虽然解决了上面提到的两个问题,但是存在一些其它的问题。如果将上述方法抽象,可以认为通过:
h = Hash(key) % N
这个算式计算每个key的请求应该被发送到哪台服务器,其中N为服务器的台数,并且服务器按照0 – (N-1)编号。
问题
设有一台服务器宕机了,那么为了填补空缺,要将宕机的服务器从编号列表中移除,后面的服务器按顺序前移一位并将其编号值减一,此时每个key就要按h = Hash(key) % (N-1)重新计算;同样,如果新增了一台服务器,虽然原有服务器编号不用改变,但是要按h = Hash(key) % (N+1)重新计算哈希值。因此系统中一旦有服务器变更,大量的key会被重定位到不同的服务器从而造成大量的缓存不命中。而这种情况在分布式系统中是非常糟糕的。
一个设计良好的分布式哈希方案应该具有良好的单调性,即服务节点的增减不会造成大量哈希重定位。一致性哈希算法就是这样一种哈希方案。
Hash 算法的一个衡量指标是单调性( Monotonicity ),定义如下:
单调性是指如果已经有一些内容通过哈希分派到了相应的缓冲中,又有新的缓冲加入到系统中。哈希的结果应能够保证原有已分配的内容可以被映射到新的缓冲中去,而不会被映射到旧的缓冲集合中的其他缓冲区。
容易看到,上面的简单 hash 算法 hash(object)%N 难以满足单调性要求。
一致性哈希算法
简介
一致性哈希算法(Consistent Hashing Algorithm)是一种分布式算法,常用于负载均衡。Memcached client也选择这种算法,解决将key-value均匀分配到众多Memcached server上的问题。它可以取代传统的取模操作,解决了取模操作无法应对增删Memcached Server的问题(增删server会导致同一个key,在get操作时分配不到数据真正存储的server,命中率会急剧下降)。
简单来说,一致性哈希将整个哈希值空间组织成一个虚拟的圆环,如假设某哈希函数H的值空间为0 – (2^32)-1(即哈希值是一个32位无符号整形),整个哈希空间环如下:

整个空间按顺时针方向组织。0和(2^32)-1在零点中方向重合。
下一步将各个服务器使用H进行一个哈希,具体可以选择服务器的ip或主机名作为关键字进行哈希,这样每台机器就能确定其在哈希环上的位置,这里假设将上文中三台服务器使用ip地址哈希后在环空间的位置如下:
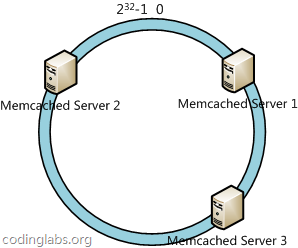
接下来使用如下算法定位数据访问到相应服务器:将数据key使用相同的函数H计算出哈希值h,通根据h确定此数据在环上的位置,从此位置沿环顺时针“行走”,第一台遇到的服务器就是其应该定位到的服务器。
例如我们有A、B、C、D四个数据对象,经过哈希计算后,在环空间上的位置如下:
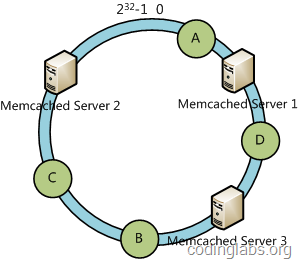
根据一致性哈希算法,数据A会被定为到Server 1上,D被定为到Server 3上,而B、C分别被定为到Server 2上。
容错性与可扩展性分析
下面分析一致性哈希算法的容错性和可扩展性。现假设Server 3宕机了:
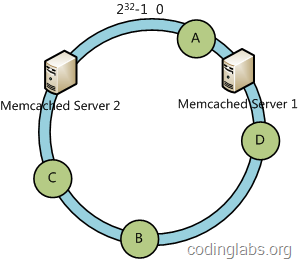
可以看到此时A、C、B不会受到影响,只有D节点被重定位到Server 2。一般的,在一致性哈希算法中,如果一台服务器不可用,则受影响的数据仅仅是此服务器到其环空间中前一台服务器(即顺着逆时针方向行走遇到的第一台服务器)之间数据,其它不会受到影响。
下面考虑另外一种情况,如果我们在系统中增加一台服务器Memcached Server 4:
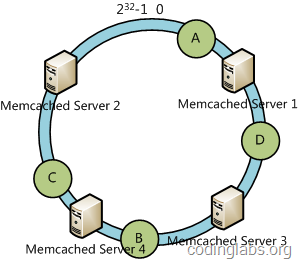
此时A、D、C不受影响,只有B需要重定位到新的Server 4。一般的,在一致性哈希算法中,如果增加一台服务器,则受影响的数据仅仅是新服务器到其环空间中前一台服务器(即顺着逆时针方向行走遇到的第一台服务器)之间数据,其它不会受到影响。
综上所述,一致性哈希算法对于节点的增减都只需重定位环空间中的一小部分数据,具有较好的容错性和可扩展性。
###3.3 虚拟节点### 一致性哈希算法在服务节点太少时,容易因为节点分部不均匀而造成数据倾斜问题。例如我们的系统中有两台服务器,其环分布如下:

此时必然造成大量数据集中到Server 1上,而只有极少量会定位到Server 2上。
引入虚拟节点
为了解决这种数据倾斜问题,一致性哈希算法引入了虚拟节点机制,即对每一个服务节点计算多个哈希,每个计算结果位置都放置一个此服务节点,称为虚拟节点。具体做法可以在服务器ip或主机名的后面增加编号来实现。例如上面的情况,我们决定为每台服务器计算三个虚拟节点,于是可以分别计算“Memcached Server 1#1”、“Memcached Server 1#2”、“Memcached Server 1#3”、“Memcached Server 2#1”、“Memcached Server 2#2”、“Memcached Server 2#3”的哈希值,于是形成六个虚拟节点:

实现
php版本
function mHash($key) {
$md5 = substr(md5($key),0,8);
$seed = 31;
$hash = 0;
for($i=0;$i<8;$i++) {
$hash = $hash * $seed + ord($md5[$i]);
}
return $hash & 0x7FFFFFFF;
}
class FlexiHash {
private $serverList = array(); //服务器列表
private $isSorted = false; //是否排过序
/**
* 添加服务器到列表
*/
public function addServer($server) {
$hash = mHash($server);
if (!isset($this->serverList[$hash])) {
$this->serverList[$hash] = $server;
}
$this->isSorted = false;
return true;
}
/**
* 从服务器列表中移除服务器
*/
public function removeServer($server) {
$hash = mHash($server);
if (isset($this->serverList[$hash])) {
unset($this->serverList[$hash]);
}
$this->isSorted = false;
return true;
}
public function lookup($key) {
$hash = mHash($key);
if (!$this->isSorted) {
krsort($this->serverList, SORT_NUMERIC);
$this->isSorted = true;
}
foreach ($this->serverList as $shash => $server) {
if ($hash > $shash) {
return $server;
}
}
return $this->serverList[count($this->serverList)-1];
}
}
java版本
package com.king.consistenthash;
import java.security.MessageDigest;
import java.security.NoSuchAlgorithmException;
import java.util.Collection;
import java.util.SortedMap;
import java.util.TreeMap;
/**
* 一致性Hash算法
*
* @param <T> 节点类型
*/
public class ConsistentHash<T> {
/**
* Hash计算对象,用于自定义hash算法
*/
HashFunc hashFunc;
/**
* 复制的节点个数
*/
private final int numberOfReplicas;
/**
* 一致性Hash环
*/
private final SortedMap<Long, T> circle = new TreeMap<>();
/**
* 构造,使用Java默认的Hash算法
* @param numberOfReplicas 复制的节点个数,增加每个节点的复制节点有利于负载均衡
* @param nodes 节点对象
*/
public ConsistentHash(int numberOfReplicas, Collection<T> nodes) {
this.numberOfReplicas = numberOfReplicas;
this.hashFunc = new HashFunc() {
@Override
public Long hash(Object key) {
// return fnv1HashingAlg(key.toString());
return md5HashingAlg(key.toString());
}
};
//初始化节点
for (T node : nodes) {
add(node);
}
}
/**
* 构造
* @param hashFunc hash算法对象
* @param numberOfReplicas 复制的节点个数,增加每个节点的复制节点有利于负载均衡
* @param nodes 节点对象
*/
public ConsistentHash(HashFunc hashFunc, int numberOfReplicas, Collection<T> nodes) {
this.numberOfReplicas = numberOfReplicas;
this.hashFunc = hashFunc;
//初始化节点
for (T node : nodes) {
add(node);
}
}
/**
* 增加节点<br>
* 每增加一个节点,就会在闭环上增加给定复制节点数<br>
* 例如复制节点数是2,则每调用此方法一次,增加两个虚拟节点,这两个节点指向同一Node
* 由于hash算法会调用node的toString方法,故按照toString去重
*
* @param node 节点对象
*/
public void add(T node) {
for (int i = 0; i < numberOfReplicas; i++) {
circle.put(hashFunc.hash(node.toString() + i), node);
}
}
/**
* 移除节点的同时移除相应的虚拟节点
*
* @param node 节点对象
*/
public void remove(T node) {
for (int i = 0; i < numberOfReplicas; i++) {
circle.remove(hashFunc.hash(node.toString() + i));
}
}
/**
* 获得一个最近的顺时针节点
*
* @param key 为给定键取Hash,取得顺时针方向上最近的一个虚拟节点对应的实际节点
* @return 节点对象
*/
public T get(Object key) {
if (circle.isEmpty()) {
return null;
}
long hash = hashFunc.hash(key);
if (!circle.containsKey(hash)) {
SortedMap<Long, T> tailMap = circle.tailMap(hash); //返回此映射的部分视图,其键大于等于 hash
hash = tailMap.isEmpty() ? circle.firstKey() : tailMap.firstKey();
}
//正好命中
return circle.get(hash);
}
/**
* 使用MD5算法
* @param key
* @return
*/
private static long md5HashingAlg(String key) {
MessageDigest md5 = null;
try {
md5 = MessageDigest.getInstance("MD5");
md5.reset();
md5.update(key.getBytes());
byte[] bKey = md5.digest();
long res = ((long) (bKey[3] & 0xFF) << 24) | ((long) (bKey[2] & 0xFF) << 16) | ((long) (bKey[1] & 0xFF) << 8)| (long) (bKey[0] & 0xFF);
return res;
} catch (NoSuchAlgorithmException e) {
e.printStackTrace();
}
return 0l;
}
/**
* 使用FNV1hash算法
* @param key
* @return
*/
private static long fnv1HashingAlg(String key) {
final int p = 16777619;
int hash = (int) 2166136261L;
for (int i = 0; i < key.length(); i++)
hash = (hash ^ key.charAt(i)) * p;
hash += hash << 13;
hash ^= hash >> 7;
hash += hash << 3;
hash ^= hash >> 17;
hash += hash << 5;
return hash;
}
/**
* Hash算法对象,用于自定义hash算法
*/
public interface HashFunc {
public Long hash(Object key);
}
}